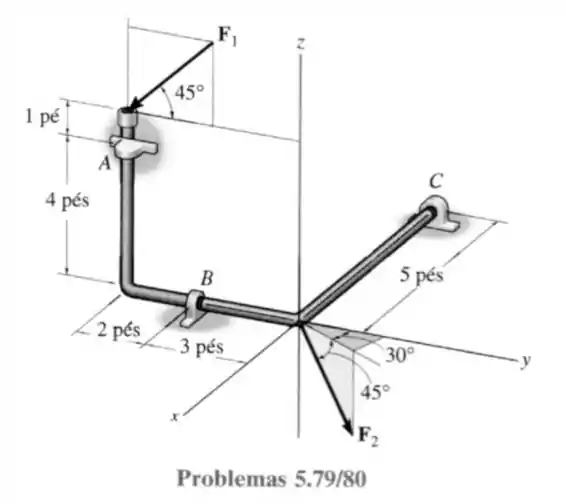
80- A barra dobrada é apoiada em e por mancais simples. Determine a intensidade de capaz de fazer a reação no mancal ser igual a zero. Os mancais estão adequamente alinhados e exercem apenas forças de reação na barra. Considere que .
Passo 1
A única diferença dessa questão para a anterior é que nessa a reação na figura abaixo vale agora .
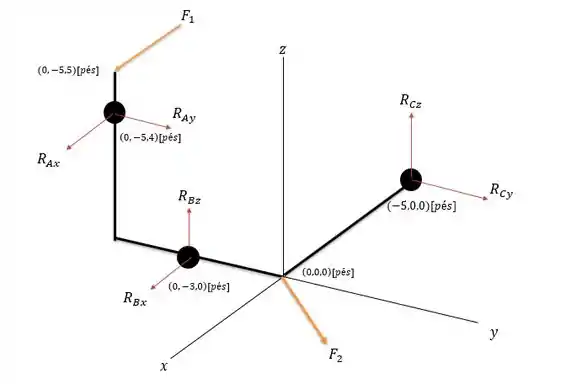
E a componente continua sendo:
Passo 2
Isso faz com que o sistema de equações passe a ser:
O que ainda continua tendo seis equações para seis incógnitas e só influência na somatória das forças, não nos momentos, uma vez que os momentos são em relação a posição dele.
Da equação podemos escrever:
Da equação temos:
Substituindo 6 em temos:
Substituindo essa última na equação temos:
Aplicando esse resultado em :
Agora substituindo os resultados que conhecemos na equação :
Substituindo em todas as equações temos: